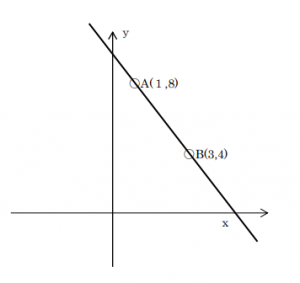
2点（A,B)の座標が分かれば直線は引けます。まず、グラフに2点をプロットして直線を引いてみると
2点を結ぶ直線が分かります（フリーハンドでOK）。このグラフで傾きが正なのか負なのか、ｙ切片が正なのか負なのかが分かります。このグラフで公式により算出した式の確認も可能です。
まずはグラフを書いてみましょう。

Plonium

A,Bの座標がわかれば、2点を結ぶ直線の式が出せます。

A(1,8）、B（3,4)を結ぶ直線の式は以下で求められます。

\((y-8)=\dfrac{4-8}{3-1}(x-1)\)
\(y=-2x+10\)

これで直線の式は出ました。この式は正解なのでしょうか？
確認するにはグラフを書いて（フリーハンドでOK)確認することが一番です。

一次関数だけではなく、二次関数も同じです。式を出したら、簡単なグラフを書いて確認してみましょう。うかっりミスが減ります。
慣れてくると頭のなかでグラフがイメージできるようになります。

Polonium

下記の複二次式の因数分解について考えてみます。
\(x^4-7x^2y^2+y^4\)

テキスト解答
\(x^4-7x^2y^2+y^4\)
\(=(x^4+2x^2y^2+y^4)-9x^2y^2\)
\(=(x^2+y^2)^2-(3xy)^2\)
\(=\{(x^2+y^2)+3xy\}\{(x^2+y^2)-3xy\}\)
\(=(x^2+3xy+y^2)(x^2-3xy+y^2)\)

別解
\(x^4-7x^2y^2+y^4\)
\(=(x^4-2x^2y^2+y^4)-5x^2y^2\)
\(=(x^2-y^2)^2-(\sqrt5xy)^2\)
\(=\{(x^2-y^2)+\sqrt5xy\}\{(x^2-y^2)-\sqrt5xy\}\)
\(=(x^2+\sqrt5xy-y^2)(x^2-\sqrt5xy-y^2)\)

別解でも因数分解の条件が無理数を含まないという場合であれば正解になると思いますが、いかがでしょうか？

Polonium

乗除の混じった計算を行う場合、中学レベルでは分子、分母に分けて実施するのが普通です。しかし、この場合、約分が必要となり計算間違いの可能性があります。
指数関数の知識を使って累乗で計算することで約分でのミスが低減できます。

【指数を用いた方法】
\(6ab\times 2a^2b\div 9a^3b^3\)
\(=6\times 2\div 9 a^{1+2-3} b^{1+1-3}\)
\(=\dfrac{4}{3b}\)

Polonium

公式は文字変数もそのまま含めて　公式でしょうか。？
それとも、内容を理解していれば変数は何でもよいのでしょうか？

例えば　解の公式でa,b,c　の変数をすべて入れ替えたような式を書いて（再定義する）
公式として認めよ、と言われたときに、

〇自分が再定義し納得して用いることは問題ない。
〇中には公式の内容を理解しないまま使う輩もいるのでそれよりは良い。
〇しかし「公式」は社会の公器でもあり、コミュニケーション・ツールでもあるので標準化されたものとして
　扱うべき。

私の考えは、公式と名がつくくらいだから社会の公器としての役割もあるのではないでしょうか。
すなわちローカルに自分だけが使う式は公式とは呼ばないわけで、意思伝達を伴うものが公式であると定義するのではないでしょうか。

自分は昔エンジニアをやってましたが、当時はJIS、MILなど多数の標準規格に囲まれて仕事をしていました。
設計、購買、製造、検査、販売、保守と多くの人との関わりからしてこれらの標準規格が重要であることがよく理解できました。

残念ながら数学教育の世界では標準規格を意識した動きはほとんど無いように感じます。しかし、数学が次第に他の産業に直接関係するようになると
そうもゆかなくなるのではないでしょうか。すなわち公式は一つの標準規格と認識すべきであると考えます。

卑近な例を一つあげると、将来彼または彼女が生徒指導側にまわったとき、公式は何でもよい、１００人いたら１００様の公式を再定義すべきだと指導するか
ということです。これでは現場に混乱と生産性低下をもたらすだけではないでしょうか。すなわち発散するわけです。

ブログの投稿の仕方を教わりました。
永く、特に図式を自由に投稿できたらいいなと思っていました。
ようやくそれが実現できそうです。

とりあえずは毎日、１件を目標にします。
よろしく。